1. Stream
给了个class Stream, 内部有一个可以call的method: read(int n)
可以从这个stream中读取数据
implement一个class multiStream
支持read(int n) add( Stream s) delete(Stream s) 三个function
2. Coupon
系统设计是在现有的打车系统上面加一个coupon功能,主要问了db要怎么改,api怎么写,如果把coupon变成一个系统要怎么做,micro-service的pros&cons。
3. Minimum Window Substring
Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there is no such substring, return the empty string "".
The testcases will be generated such that the answer is unique.
A substring is a contiguous sequence of characters within the string.
Example 1:
Input: s = "ADOBECODEBANC", t = "ABC" Output: "BANC" Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.
Example 2:
Input: s = "a", t = "a" Output: "a" Explanation: The entire string s is the minimum window.
Example 3:
Input: s = "a", t = "aa" Output: "" Explanation: Both 'a's from t must be included in the window. Since the largest window of s only has one 'a', return empty string.
Constraints:
- m == s.length
- n == t.length
- 1 <= m, n <= 105
- s and t consist of uppercase and lowercase English letters.
Follow up: Could you find an algorithm that runs in O(m + n) time?
4. Time-Based Key-Value Store Design 
Design a time-based key-value data structure that can store multiple values for the same key at different time stamps and retrieve the key's value at a certain timestamp.
Implement the TimeMap class:
- TimeMap() Initializes the object of the data structure.
- void set(String key, String value, int timestamp) Stores the key key with the value value at the given time timestamp.
- String get(String key, int timestamp) Returns a value such that set was called previously, with timestamp_prev <= timestamp. If there are multiple such values, it returns the value associated with the largest timestamp_prev. If there are no values, it returns "".
Example 1:
Input
["TimeMap", "set", "get", "get", "set", "get", "get"]
[[], ["foo", "bar", 1], ["foo", 1], ["foo", 3], ["foo", "bar2", 4], ["foo", 4], ["foo", 5]]
Output
[null, null, "bar", "bar", null, "bar2", "bar2"]
Explanation
TimeMap timeMap = new TimeMap();
timeMap.set("foo", "bar", 1); // store the key "foo" and value "bar" along with timestamp = 1.
timeMap.get("foo", 1); // return "bar"
timeMap.get("foo", 3); // return "bar", since there is no value corresponding to foo at timestamp 3 and timestamp 2, then the only value is at timestamp 1 is "bar".
timeMap.set("foo", "bar2", 4); // store the key "foo" and value "bar2" along with timestamp = 4.
timeMap.get("foo", 4); // return "bar2"
timeMap.get("foo", 5); // return "bar2"
Constraints:
- 1 <= key.length, value.length <= 100
- key and value consist of lowercase English letters and digits.
- 1 <= timestamp <= 107
- All the timestamps timestamp of set are strictly increasing.
- At most 2 * 105 calls will be made to set and get.
5. Range Sum Query 2D - Immutable
Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Implement the NumMatrix class:
- NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
- int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Example 1:
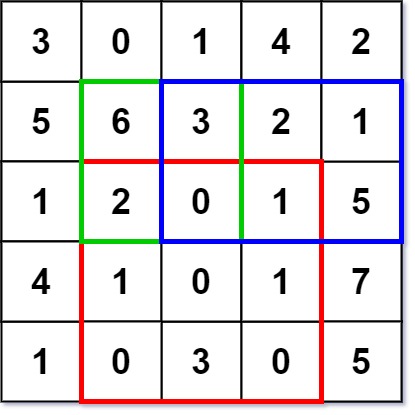
Input ["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]] Output [null, 8, 11, 12] Explanation NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 200
- -105 <= matrix[i][j] <= 105
- 0 <= row1 <= row2 < m
- 0 <= col1 <= col2 < n
- At most 104 calls will be made to sumRegion.


