1. Maximum Path Sum in Binary Tree
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example 1:
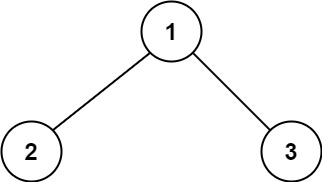
Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
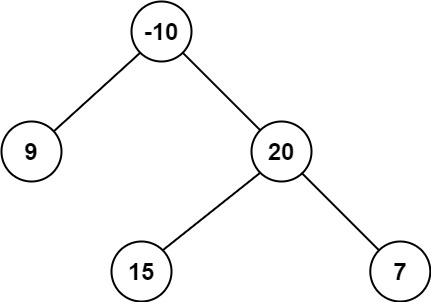
Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range [1, 3 * 104].
- -1000 <= Node.val <= 1000
2. ThreeSum Problem
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
Example 1:
Input: nums = [-1,0,1,2,-1,-4] Output: [[-1,-1,2],[-1,0,1]] Explanation: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0. nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0. nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0. The distinct triplets are [-1,0,1] and [-1,-1,2]. Notice that the order of the output and the order of the triplets does not matter.
Example 2:
Input: nums = [0,1,1] Output: [] Explanation: The only possible triplet does not sum up to 0.
Example 3:
Input: nums = [0,0,0] Output: [[0,0,0]] Explanation: The only possible triplet sums up to 0.
Constraints:
- 3 <= nums.length <= 3000
- -105 <= nums[i] <= 105
3. Alternative Solution to a Problem
In the fourth round of an onsite interview, after presenting your initial solution to a problem, you are asked if there is a more straightforward (possibly less efficient) way to solve it, prompting you to write a brute force solution.
4. Minimum Number of Sprinklers to Water a Garden
Given an array representing a garden, where the value at each index represents the range of the sprinkler at that position, determine the minimum number of sprinklers that need to be turned on to water the entire garden. The garden is represented as a 1 to N array, and the range of each sprinkler is given by the array values. Describe a greedy algorithm to solve this problem and discuss its efficiency.
5. String Compression Algorithm
Design an algorithm to compress a given string by describing the total number of consecutive occurrences of each character next to it. For example, the string 'abaasass' should be compressed to 'aba2sas2'. If a character occurs only once, it is added to the compressed string. If it occurs consecutive times, the character is followed by an integer representing the number of consecutive occurrences. Implement the function compressedString that returns the compressed form of a message.


