数据科学家被哈佛商业评为21世纪最具新引力的职业之一。

这并非空穴来风，近十年以来，数据科学家一直站在聚光灯下，人工智能专家的收入一定程度上可以与体育明星一较高下。

在这场追求名利的浪潮中，许许多多从业人士在这场热潮中熙熙攘攘，以尽快获得数据科学家的title。

各种各样割韭菜方式层出不穷，满眼的“AI入门到精通”的网络教程都在教你如何在21天成为一名数据科学家，并且不需要你看一眼数学公式；数据科学顾问许诺一旦采纳他们的方案，可以为公司带来百万美金的回报，每个人都赚得破满钵满。

事实真的如此吗？数据科学是什么？数据科学和AI是什么关系呢？

在这个小学生都可以顺口溜出几个大数据的名词的时代中，我们的很多领域专家依旧在延续着“传统”的数据分析之道上进行耕耘：经济学家尝试各种方式研究教育程度如何影响收入、生物统计学家试图解释饱和脂肪如何导致心脏病、心理学家试图分析肯定的话与幸福婚姻的关系。

我们想说的是数据科学家并不是一个新兴领域，只是由于媒体的大肆营销和宣传，这一职业才进入了大众视野，从而显得很“年轻”。

如果平时喜欢喝啤酒，你最终会发现，在倒酒姿势正确的前提下，酒杯中会呈现下面的状态：

酒杯中表面有一层泡沫，最终会破灭（啤酒越好，持续时间越长）；

酒杯下面绝大多数是啤酒，这层才是口感最好的部分。

为什么说啤酒这个例子呢？因为但凡媒体鼓噪的领域均存在不同程度的泡沫，现在数据科学、人工智能的热潮也不会例外。只有泡沫破灭，最有价值的部分（啤酒）才会显露出来，这个才是数据科学、人工智能真正的归宿和价值所在。

在成为数据科学家（姑且这么叫吧）、人工智能从业者这条路上，也不存在什么捷径，更不要去信21天称为人工智能专家的规划，培训机构的镰刀时刻向你敞开。

作为一个数据科学的入门选手，最基本的操作应该是避开哪些泡沫、避免成为韭菜，数学和统计学是绕不开的知识壁垒，持续不断的学习能力也是绕不开的话题，加油！

目前大家谈论的机器学习算法都是Predict-based的算法，这类算法非常擅长解决的事情是预测问题，利用机器学习算法解决问题的唯一要求是将问题定义为预测问题：

识别人脸，构建一个 ML 模型，该模型预测图片中是否存在人脸；

识别是否点击广告，构建一个CTR模型，模型预测该广告是否被点击。

Predict-based的机器学习算法虽然普适性很好，但是基本是基于目标和特征的相关性进行决策，决策结果可能会带来一些问题：在许多行业中，低价格与低销量呈现相关性，如酒店行业，旅游旺季以外的时候价格低，而需求旺盛、酒店爆满时价格高。

Predict-based的机器学习算法决策的结果可能是一个ML模型的预测结果可能表明提高价格会导致酒店出售更多的房间。

Predict-based的机器学习算法在这种逆因果关系类型的问题上显得力不从心。

因为它们要求我们回答“what if”问题，经济学家称之为反事实(counterfactual)，这些例子在现实空间不可能存在，除非我们有一个平行空间供我们选择：

如果我目前商品的定价不是这个价格，而是使用另一个价格，会发生什么情况？

如果我不再进行低脂饮食，而是改为低糖饮食，会发生什么？

这些问题的核心在于我们希望研究现象与效果之间的量化关系，现有的相关性模型不能够满足因果性研究的需求，从而引出了一个新的AI分支--因果推断。

因果推断是在一个较大系统内部确定指定现象（因）的实际、独立效果（果）的过程。因果推断和相关性推断的主要区别是前者分析结果变量在其原因变量变化时发生的回应。研究事物起因的科学则称作原因论。因果推断可给出因果关系推理建立的因果关系模型的证据

因果问题在日常问题中随处可见：

例如销售公司如何提高销售额？

移民是否会降低个人找工作的机会（移民是否会导致失业率上升）？

向穷人汇款会降低犯罪率吗？

不管你在哪个领域，很可能你也需要处理某种类型的因果问题，因果推断就成为我们研究这些因果问题的有效手段。

从common sense的角度，很容易理解为什么相关不是因果关系，但是如何量化和解释这种因果性的关系是一个需要深入研究的话题：

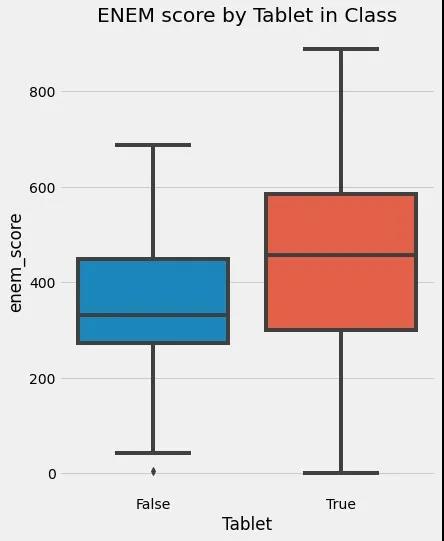
如果有人告诉你，给学生提供平板电脑的学校比不给学生提供平板电脑的学校学生成绩更好。你可能会很快指出，有平板电脑的学校更有钱、师资好等因素是导致成绩好的原因，即使没有平板电脑，它们也会比平均水平的学校成绩更好。所以不能得出结论，给孩子提供平板电脑会提高他们的学习成绩。

所以在这个case上，只能说学校提供平板电脑与成绩表现正相关。

在深入探讨之的过程中，引入的变量名如下：

i：表示第 i个体(unit)；
Ti：对个体 i施加的干预(treatment)；
Yi:表示在个体 i上观察到的结果（outcome）输出，也就是因果推断的果
Y0i:表示个体 i没有施加Treatment的潜在结果(potential outcome)；
Y1i:表示个体i 施加Treatment的潜在结果(potential outcome)。

上面提到的考试成绩的问题中，关键问题是我们如何量化平板电脑T 对学习成绩Y 的影响，但是现实的约束是在于我们永远无法同时观察到在同一个体上施加干预和不施加干预的结果，这也导致了因果性问题的复杂度远超于Predict-based的机器学习算法。

那我们应该如何解决这种counterfactual约束呢？在因果性问题的研究过程中，经常会提到potential outcomes这一概念。之所以称为potential，是因为 Treatment 并未发生下的 outcome（counterfactual）：

潜在结果模型(Potential Outcomes Model)是其中最重要的理论模型之一，其核心是比较同一个研究对象(Unit)在接受干预(Treatment)和不接受干预(Control)时结果差异，认为这一结果差异就是接受干预相对于不接受干预的效果。对于同一研究对象而言，通常我们不能够既观察其干预的结果，又观察其不干预的结果。对于接受干预的研究对象而言，不接受干预时的状态是一种“反事实”状态；对于不接受干预的研究对象而言，接受干预时的状态也是一种“反事实”状态；所以该模型又被某些研究者称之为反事实框架(Counter factual Framework)。潜在结果模型的主要贡献者是哈佛大学著名统计学家唐纳德·鲁宾(Donald B.Rubin)，因此该模型又被称为鲁宾因果模型(Rubin Causal Model)。

不过，鲁宾(Rubin，2005)并不认同“反事实框架”的概念，他认为结果的出现与否主要取决于干预机制(Assignment Mechanism)，这并不意味着一种结果不存在，只是我们事实上只能够看到一种结果。

对于鲁宾而言，潜在结果是一个更合适的概念。考虑到这一理论主要是由鲁宾开创并持续推动这一研究，我们在介绍该理论时，也使用了潜在结果模型的概念。